Introduction
The hippocampal trisynaptic circuit and extensive connections with entorhinal cortex neurons form a microcircuit that is crucial in spatial memory encoding, storage and recall (Remondes & Schuman, 2003). Dentate gyrus (DG) plays a key role especially in the pattern separation and distinction paradigms (Chavlis et al., 2017; Marr, 1971; Santoro, 2013; Treves & Rolls, 1994; Yassa & Stark, 2011). In mammals, adult neurogenesis in the subgranular zone of DG has the potential of generating adult-born (AdB) immature granule cells (GC) that can be integrated into the DG circuitry and modulate the activity in the region (Coulter & Carlson, et al., 2007). The adult-born (AdB) immature neurons have distinct morphological and biophysical features when compared to embryonic-born mature granule cells (GCs), which rises several questions about their contribution to the regional function (Zhao et al., 2006; Llorens-Martin et al., 2015; Llorens-Martin et al., 2016).
The elliptical cell body of the mature DG GC is 10-18 μm in diameter (Amaral et al., 2007). The apical dendrites of GC extend and branch into the molecular layer, where the axonal projections from entorhinal cortex (EC) cells, i.e. layer II stellate cells, reach to form glutamatergic synapses (Zhou et al., 2004). GC axons branch extensively throughout the hilus as they project further to contact CA3 pyramidal neuron apical dendrites (Lee et al., 2014). The nonmyelinated GC axons with several collaterals (a.k.a. mossy fibers) also communicate heavily with the interneurons around the GC layer. Among the interneurons of DG, parvalbumin-positive (PV) basket cells and somatostatin-positive interneurons are known to regulate GC activity through reciprocal connections (Lee et al., 2014).
The GC morphology (i.e., dendritic and axonal branching patterns) (Figure 1) and its wide range of connections (e.g., mossy fibers projecting to the CA3 region) allow them to filter perforant pathway inputs arriving in the molecular layer of DG and project signals to the CA3 selectively. Here, they play a key role in pattern separation, which ensures similar input patterns are stored as distinct representations in the hippocampus (Yassa & Stark, 2011). The unmyelinated axons of GC with dense collaterals form the mossy fibers that project to the apical dendrites of CA3 pyramidal neurons.
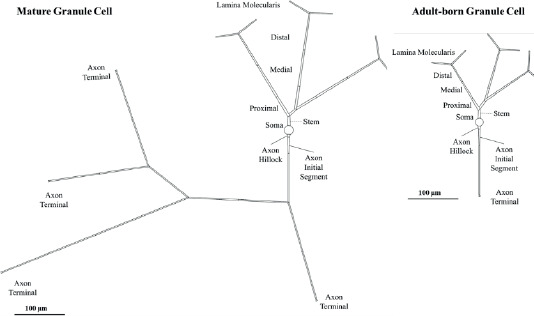
Figure 1. DG Mature GC and Immature AdB GC Model Morphologies. Simplified topologies of mature and adult-born granule cells derived from averaged morphologies in rodent GC samples (Chavlis et al., 2017). These topologies are schematic representations used for compartmental modeling purposes and do not correspond to direct reconstructions. In both models, the proximal segment on the right branches into two, where the segment prior to the branching point is titled as Proximal I and the segment after the branching point is titled as Proximal II. Mature GC axon has three branching points: (1) Immediately after the first axonal segment, where the right branch (axon.R) consists of two axonal segments and an axon terminal, (2) after the second segment on the left branch (axon.L), followed by a four-segment long left branch (axon.LL) ending with an axon terminal, and a right branch (axon.LR), (3) after the first segment of axon. LR, each branch has two axonal segments ending with axon terminals. Immature AdB GC has only one axonal segment followed by an axon terminal.
AdB GCs have initial electrophysiological characteristics different from mature GCs. They have a higher input resistance, lower voltage thresholds, and slower membrane time constants (Amaral et al., 2007). They are also more prone to LTP (Espósito et al., 2005; Laplagne et al., 2006). Input resistance for mature GCs is around 100-300 MΩ, where it can be as high as 4GΩ for AdB GCs (Heigele et al., 2016). GCs have reduced ion channels that open at resting potential, such as inward-rectifier potassium channels (Kir). The kinetics of Kir, as well as dendritic and axonal processes, increase the input resistance of immature neurons up to 1 GΩ (Liu et al., 1996; Schmidt-Hieber et al., 2004). Another distinctive feature of AdB GCs is the short-term expression of T-type calcium channels, which underlies the sudden voltage spike caused by low-threshold calcium induced by physiological conditions (Goncalves et al., 2016). However, mature GCs are unable to produce calcium-induced voltage spikes to a low threshold and no significant sodium-induced voltage spikes are seen when pharmacologically blocking T-type channels (Schmidt-Hieber et al., 2004). Action potentials initiated by sodium currents trigger short-term calcium currents with a high amplitude in both mature and AdB GCs (Stocca et al., 2008). However, AdB GCs can perform temporal summation of inputs more efficiently than mature GCs because they show longer-lasting temporal wave spikes in their proximal and distal dendrites (Stocca et al., 2008). Differences in calcium currents may also result from synaptic plasticity. Dendrites of mature GCs are generally described as passive integrators that strongly dampen voltage signals (Krueppel et al., 2011). As a consequence, the amplitude of the backpropagating action potential is attenuated throughout the dendrites of mature GCs, and excitatory postsynaptic potentials (EPSPs) show a steep decline from the dendrites to the soma.
Our focus on morphology in the model is to study structural characteristics without delving into other functional aspects. Morphological analysis provides valuable insights into the physical organization and development of cells, which is crucial for understanding how these structures relate to overall neural activity and behavior. Focus on morphology helps to examine how variations in cell shape, size, and organization contribute to broader cognitive and physiological processes. This approach allows for a more controlled and specific investigation of the structural factors involved.
Materials and methods
The model construction and simulations were performed in a Python environment with the Brian2 module (Stimberg et al., 2019). The analyses were performed with user-defined functions in Python, partially utilizing Brian2. The morphological parameters were gathered through a survey of in vitro and in vivo experimental findings and reduced into a simplified multi-compartmental topology that reflects the main branching patterns. Simulations were run with a time step Δt = 0.01 ms and the implicit backward Euler integration. The voltage traces were recorded from the midpoint of every compartment. All custom scripts and simulation codes used in this study will be shared publicly through ModelDB or GitHub to ensure transparency and reproducibility.
Morphological design
The model topology and morphological parameters are determined by a comparative analysis of existing experimental and computational studies. The morphologies used to construct simplified topological models in Figure 1 were derived from Chavlis et al. (2017), specifically granule cells of the dentate gyrus from rats. We included a total of 2 granule cells as adults born (very early developmental stage) and mature. These morphologies were chosen to represent the morphologically most diverse developmental stages and ensure consistent topological comparison. The most striking morphological difference between mature and AdB GCs is the length and branching of the axon, which was reflected in the reduced topology of our models. For dendritic branching, we adapted the 3-dendrite model of Chavlis et al. (2017), with shortened segment length in AdB GCs. The general topology of the morphological parameters for each compartment of GCs is given in Table 1.
Table 1. Morphological parameters of DG GC models.
| Mature GC | Immature AdB GC | ||||||
|---|---|---|---|---|---|---|---|
| Length (µm) | Initial Diameter (µm) | End Diameter (µm) | Length (µm) | Initial Diameter (µm) | End Diameter (µm) | ||
| Soma | 12 | 12 | - | 10 | 10 | - | |
| Dendrite | Stem | 1 | 3 | 1.9 | 1 | 3 | 1.9 |
| Proximal I | 20 | 0.95 | 0.95 | 20 | 1 | 0.95 | |
| Proximal II | 55 | 0.95 | 0.9 | 25 | 0.95 | 0.9 | |
| Medial | 75 | 0.9 | 0.8 | 45 | 0.9 | 0.8 | |
| Distal | 75 | 0.8 | 0.8 | 45 | 0.8 | 0.8 | |
| Lamina Moleculare | 50 | 0.8 | 0.8 | 25 | 0.8 | 0.8 | |
| Axon | Axon Hillock | 10 | 1.5 | 1.3 | 10 | 1.5 | 1.3 |
| Axon Initial Segment | 40 | 1.3 | 1 | 40 | 1.3 | 1 | |
| Axonal Segment | 100 | 1 | 1 | 100 | 1 | 1 | |
| Axon Terminal | 4 | 1 | 2 | 4 | 1 | 2 | |
Detailed topology of the models is given in Figure 1.
Biophysical model
The conductance-based model was designed as
where the membrane capacitance,Cm, was 0.88 μF/cm2 for AdB GC and 1μF/cm2 for mature GC. The membrane current, Im, consisted of Hodgkin-Huxley type Na+ ,K+ and leak conductances as
where the leak conductance, gL, was 0.0003 S/cm2 and the specific KV channel conductance, gK, was 0.036 S/cm2 for all compartments. The density distribution of NaV channels are reflected on the specific channel conductance, gNa , as 0.05 S/cm2 for soma, 0.5 S/cm2 for AIS and NR, and 0.005 S/cm2 for dendrites. The reversal potentials were EL = -76.5 mV , ENa = 50 mV and EK = -90 mV.
The gating kinetics for any voltage-gated channel was defined as the activation and inactivation rates of channel subunits as
where z is a generalized gating particle. The gating kinetics for NaV was defined over the activation (m) and inactivation (h) functions, whereas KV was defined with a singular activation (n) function as follows (Aradi & Holmes, 1999) :
Current injection
In order to mimic the rheobase activity driven by baseline ionic current load at a given time, a sustained constant current (Iinj) was placed at the soma for each cell. The measurements for the characterization of action potential waveforms are performed on voltage traces from soma and axon initial segment (AIS) with the minimum input current required for generating an action potential, Iinj = Imin. Firing rate responses and frequency-current plots were also obtained under constant current, increased with repeated tests with a current increment ΔI for a duration of T = 200 ms for each step.
Model response analysis
Action potential waveform characteristics. We defined the characteristics of each cell’s action potential waveform over threshold potential (Vthr), onset rapidness (ρ), peak potential (Vpeak) and action potential width (Δt1/2). Vthr was measured as the voltage at the time when reaches and exceeds 10 V/s (Naundorf et al., 2006; Oz et al., 2015).. The action potential half amplitude (V1/2) was measured as the half difference between Vpeak and Vthr, and Δt1/2 was estimated as the full width of action potential at V1/2. The two methods used to measure ρ were the inverse full width at half maximum (IFWd2) and the inverse half width at half maximum (IHWd2) of d2V/dt2 peak as described by Aldohbeyb et al. (2021).
Action potential propagation. The delay of action potential propagation from AIS to other compartments (td) was measured as td = t1/2,I - t1/2,AIS where Vm (t1/2,I) = V1/2,i at compartment “i”. The attenuation of action potential amplitude was recorded by the attenuation of Vpeak (Vpeak,i) at compartment “i” as Vpeak,i=Vpeak,AIS - Vpeak,i. Both td and Vpeak,i were plotted over the distance to the center of AIS from the center of the respective compartments. The velocity of dendritic (νd) and axonal (νa) propagation was estimated by fitting a (x, td) plot with a linear function, x = ν t + a, where a is a constant.
Frequency-current plots. The frequency – current (fI) plots were obtained by injecting a step-wise increasing constant current for 200 ms intervals, starting with Iinj < Imin. And increasing with the increment ΔI. The firing frequency was estimated over the somatic voltage traces.
The action potentials (APs) from soma and axon initial segment (AIS) of mature and AdB GCs were recorded under constant current injection at the soma (Iinj = Imin), which resulted in a 10 Hz firing rate. The changes in Vpeak, for AdB and mature GCs are given in Table 2.
Table 2. Action potential waveform characteristics for mature GC and immature AdB GC models.
| SOMA | AIS | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Vpeak (mV) | Vthr (mV) | V1/2 (mV) | Δt1/2 (ms) | ρ(IFWd2) (ms-1) | ρ(IHWd2) (ms-1) | Vpeak (mV) | Vthr (mV) | V1/2 (mV) | Δt1/2 (ms) | ρ(IFWd2) (ms-1) | ρ(IHWd2) (ms-1) | |
| Mature | 34.5 | -37.4 | -1.4 | 0.46 | 12.5 | 33.3 | 46.1 | -37.4 | 4.3 | 0.66 | 25 | 50 |
| GC | ||||||||||||
| AdB GC | 34.7 | -39.8 | -2.5 | 0.48 | 20 | 33.3 | 47.6 | -39.8 | 3.9 | 0.66 | 25 | 33.3 |
Results and discussion
The goal of this study was to reveal how the distinct morphological features of adult-born granule cells (AdB GCs) impact neural response characteristics. To this end, we constructed conductance-based models of both AdB and mature GCs using reduced topologies that emphasize their most distinctive morphological difference—axon length and branching patterns (Zhao et al., 2006). By implementing identical biophysical parameters across both models, we isolated the effect of morphology and eliminated confounding influences from intrinsic membrane properties.
Interestingly, our results showed that AdB GCs achieved firing rates similar to those of mature GCs in response to increasing constant input current. Additionally, parameters such as somatic backpropagation delay, dendritic propagation, and signal attenuation were comparable across the two models. This finding aligns with previous studies reporting that smaller somatic size and less dendritic arborization in AdB GCs lead to lower capacitance and faster signal conduction (Brunner et al., 2014), while mature GCs exhibit greater capacitance and slower temporal dynamics. Schmidt-Hieber et al. (2004) also demonstrated that the current threshold is lower in AdB GCs (141 ± 12 pA) compared to mature GCs (234 ± 9 pA), which typically corresponds to a lower voltage threshold, consistent with our observation of higher excitability in AdB GCs.
Although our models revealed no significant differences in propagation rates or frequency-current (f-I) relationships, this may be due to the simplified biophysical characteristics. Thomas et al. (2009) showed that variations in sodium and potassium channel gating kinetics significantly influence firing dynamics in more detailed models. The use of identical channel kinetics in our approach likely explains the lack of divergence in f-I curves, a finding also supported by Tejada & Roque (2014).
Recent modeling frameworks such as TREES-to-NEURON (T2N) offer enhanced integration of complex morphologies with compartmental biophysics (Beining et al., 2017), supporting more realistic simulations of AdB and mature GC function. However, in this study, the use of a reduced, yet representative multi-compartmental morphology combined with a simplified Hodgkin-Huxley (HH) type limited to Na+ and K+ currents allowed us to focus on morphological contributions while minimizing the variability introduced by differing ion channel dynamics.
Action potential waveform characteristics
The APs from soma and AIS of mature GC and immature AdB GCs were recorded under constant current injection at the soma, which resulted in a 10 Hz firing rate. The changes in Vpeak, Vthr, Δt1/2 and ρ according to two different methods (IFWd2 and IHWd2) for AdB and mature GCs are given in Table 2. Vpeak is 34.5 mV for mature GCs and 34.7 mV for immature AdB GC. The timing of AP is also slightly different, with mature GC initiating a spike slightly later than AdB GC (Figure 2-A and C). For AIS, Vpeak for mature GC is 46.1 mV and 47.6 mV for immature AdB GC. This indicates that strong depolarization occurs at AIS for both groups, with a slightly higher maximum potential in AdB GC. Vthr is approximately -37.4 mV for mature GC and approximately -39.8 mV for AdB GC both in soma and AIS. This indicates the higher excitability of immature AdB GC. Moreover, the V1/2 is -2.5 mV for AdB GC and -1.4 mV for mature GC, which implies that AdB GC might have a faster depolarization phase. The Δt1/2 values for both models are similar at the soma and AIS. For the onset rapidness (ρ), the IFWd2 method yielded a notable difference between AdB (20 ms-1) and mature GCs (12.5 ms-1), which indicates sharper AP onsets for immature AdB GC at soma (Figure 2-B).
Figure 2. Action Potentials and Phase Plots from mature GC and immature AdB GCs. Black: Mature GC, Red: Immature AdB GC. A-B: Soma, C-D: AIS.
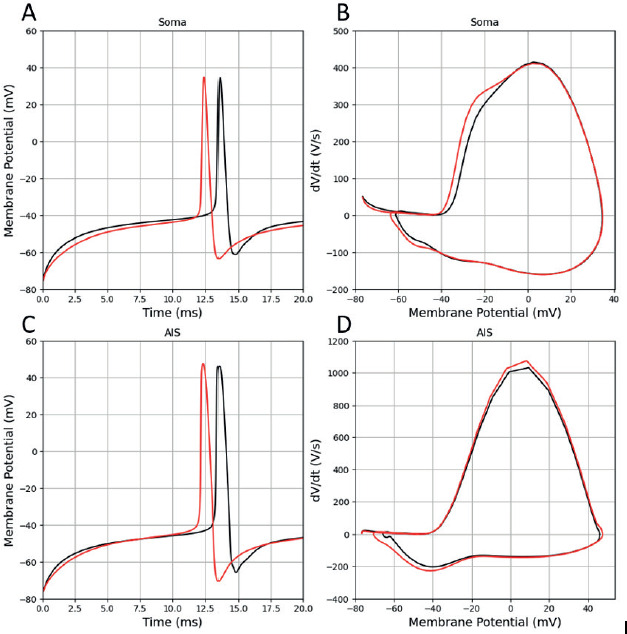
Immature AdB GC displayed a slightly higher peak depolarization velocity () compared to mature GC in AIS (Figure 2-D). AdB GC also displayed a steeper depolarization rate () at soma compared to the mature GC (Figure 2-B). It was previously shown that AdB GCs are hyperexcitable and display a faster depolarization phase compared to mature GCs (Vyleta & Snyder, 2023), which is in agreement with our findings.
In our immature AdB GC model, the length of the axon is considerably shorter and can not reach to CA3. The model was designed to reflect the early phases of immature AdB GCs, where they strictly limit their communication to local interneurons. It has been suggested that the excitability of GCs decreases with maturation, and they become tightly coupled to inhibitory circuits (Brunner et al., 2014). Our findings also replicate this notion and may indicate that the morphological differences between immature AdB and mature GC models may be sufficient to reproduce the higher excitability of AdB GC.
Frequency-current relationship
The f-I curve (Figure 3) shows how the firing rate coupled to the injected current amplitude. Both models display a Type I respond, with a nonlinear increase in frequency as the amplitude of the current injection increases. At low input current increments, the increase in firing rate grows relatively fast, while at higher input current increments the increase becomes slower approaching saturation.
Figure 3. Frequency-current amplitude curves for mature GC and immature AdB GCs. The dotted lines represent the curve fitting as explained in the text.
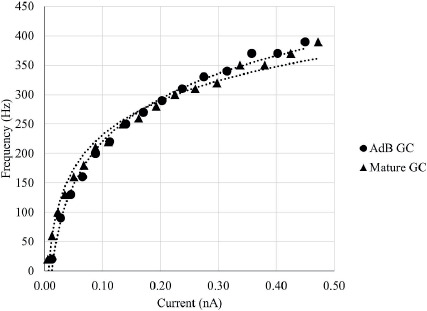
The firing rate (f) in response to current (I) injection were fit with the function f = fh* ln(I) + flimit using least square method with Levenberg-Marquadt algorithm, where fh is the inflection frequency and flimit is the saturation frequency. The variables and root mean square deviation (RMSD) for mature and immature AdB GCs are given in Table 3. The f-I curves for mature GC and immature AdB GCs slightly differ in fh and flimit. The fh of immature AdB GC is slightly lower than mature GC, however, the firing rates converge, showing that the two cell types exhibit similar maximal firing capacities at higher currents.
Table 3. Frequency-Current Plot Curve Fitting Parameters. fh : Inflection frequency, flimit : Limiting saturation frequency, RMSD : Root mean square deviation for least square method.
| fh | flimit | RMSD | |
|---|---|---|---|
| Mature GC | 105.2 | 462.45 | 0.9923 |
| AdB GC | 83.714 | 424.27 | 0.9781 |
Action potential propagation
The delay (Δtd) of AP propagation from AIS to other compartments was measured as Δtd = t1/2,i - t1/2,AIS where Vm,i(t1/2) = V1/2,i at the midpoint of the AP in compartment ‘i’. Linear regression was performed to calculate the velocities of dendritic (νd) and axonal (νa) AP propagation by fitting (x, Δtd) plot with the function x = ν t + a, where a is a constant (Table 4). Mature GC and immature AdB GCs show increased delay with increasing distance from AIS (Figure 4-A and B), where immature AdB GC exhibits slower dendritic back-propagation compared to mature GC (Table 4). The high νa for immature AdB GC might be due to the shorter and non-branching axon of this model compared to mature GC.
Figure 4. Distance-dependent (x,t) delay in action potential propagation for mature GC (A) and immature AdB GC (B).
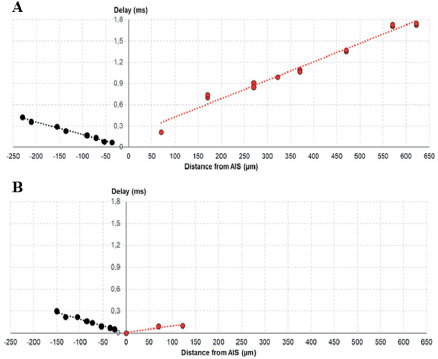
Table 4. The velocity of dendritic (νd) and axonal (νa) propagation for mature GC and immature AdB GC.
| νd (μm/ms) | ν a μm/ms) | |
|---|---|---|
| Mature GC | 560.21 | 337.57 |
| AdB GC | 523.69 | 1045.1 |
The attenuation of AP amplitude (ΔVpeak,i) across dendritic and axonal compartments was calculated by the attenuation of Vpeak,i at compartment “i” as ΔVpeak,i = Vpeak,AIS - Vpeak,i. Both GCs exhibit a decrease in dendritic Vpeak as distance increases (Figure 6), but there is no significant difference between both models. This implies that AdB GC display similar performance in dendritic backpropagation in terms of signal integrity and propagation efficiency.
Figure 5. Delay–dependent distance (t,x) in action potential propagation for mature GC and immature AdB GC. Dendritic propagation is given in (A) and axonal propagation in (B).
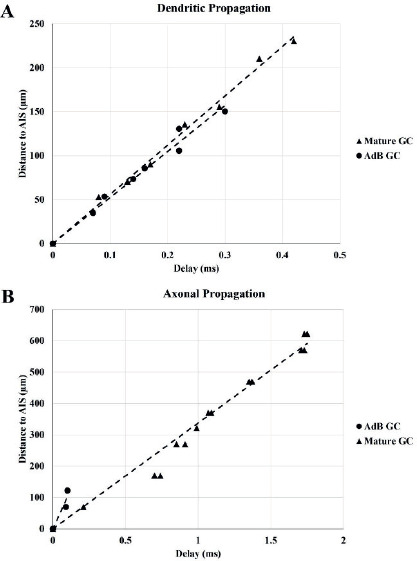
Figure 6. Vpeak -dependent (t-x) distance in action potential propagation for mature GC (A) and immature AdB GC (B).
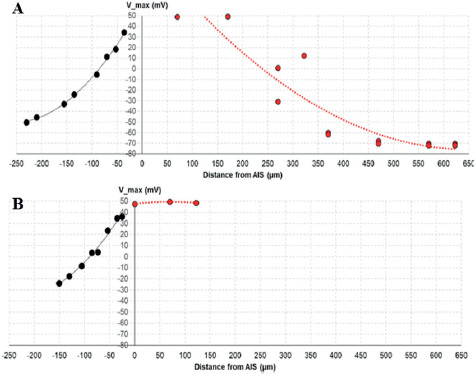
Figure 7. The dendritic peak AP amplitude attenuation in GC models.

For our goal, the use of the HH model allowed for precise isolation of ionic dynamics because it provides a biophysically simplified conductance-based model. Keeping the biophysical parameters constant in both models was essential for isolating and addressing how distinct morphological features impact the neural response characteristics. Compared to more advanced models, such as T2N (Beining et al., 2017) and SAS (Santhakumar et al., 2005), our models certainly have limitations, e.g., our model does not focus on biophysical properties where it focuses on morphological comparison.
Conclusions
Morphological differences between mature and AdB GCs have been shown to have an impact on dentate gyrus functionality. In particular, structural differences such as dendrite branching and sizes of compartments have provided insight into how these cells play different roles in information processing. Future research should focus on the axonogenesis and the maturation stages of the AdB GC model, as it would be helpful in understanding how the change of response and excitability during their integration into the hippocampal network. Additionally, exploring how the ratio of AdB GCs in the total GC population in DG influences the microcircuit response and hippocampal function can explain the balance between circuit stability and responsiveness. Investigating an optimal neurogenesis range may reveal critical thresholds for therapeutic interventions in conditions such as depression, epilepsy, and age-related cognitive decline.